Zlib's inflate algorithm
29 December 2007 an Ocaml-only implementation of Zlib’s inflate algorithm (RFC 1951) more...Zlib's inflate algorithm
closeSo I wrote one. The source code is available (under the BSD licence).
It’s pretty compact: about 250 lines of code, including comments. Usage is very simple: pass a string containing data compressed with the
zlib deflate algorithm, and a string large enough to contain the decompressed data, and it returns the same string with the decompressed data.
uncompress -> string -> string -> string. I added a small, simple example to uncompress gzipped files.
The code is based more or less on the specs, with a peek every now and then at Andrew Church’s tinflate.c when I got stuck on some ambiguity or other. It’s pretty compact - 200 lines of code - and pretty slow: gunzip beats it by a factor of 10 to 100. Maybe if I have time I’ll try and optimize it.
Finite state machine demo
13 December 2007 Animating the opening and closing of lift doors using finite state machines. more...Finite state machine demo
closeA finite state machine consists of a finite number of states, and a transition function which, given a state and an input, results in another state and an output.
An example of a simple FSM is a door, such as can be found in an elevator. Such a door requires a push on a button to open it. It opens, remains open for a short period of time, and then automatically closes again.
Normally, such a door would be modelled with two states, Open and Closed, and two transitions: from Closed to Open after a push on the button, and from Open to Close after a time out.
However, I would like to implement such a door as simply as possible. If I were to represent a door as a collection of states, there has to be a state available at any given time. So I use four states: Open, Closing, Closed, and Opening. At any given time the door is in one of these four states. A transition from one state to another is instantaneous. The states themselves, however, have duration. For instance, it takes some time for the door to open or close; once open the door will close after some time, and once closed it remains that way until someone presses a button.
A simple implementation in 20 lines of Ocaml can be found here.
The demo takes up another 27 lines of code. (Excluding comments). Compile with ocamlc graphics.cma unix.cma test.ml -o test and run;
press a mouse button to open the door. The doors take 3 seconds to open or close, and an open door will start closing again after 5 seconds.
Triangle-triangle collision detection
8 August 2007 Implementation of the canonical triangle-triangle intersection test algorithm by Thomas Moeller. more...Collision detection algorithm
closeCollision detection is an important part of any physical simulation. The basis is formed by the intersection of primitives, and the triangle-triangle intersection test is one of the most commonly used tests.
As described in Thomas Moeller, A fast triangle-triangle intersection test," J. Graphics Tools 2(2) 25-30 1997:
Let the two triangles be T1 and T2. If T2 lies strictly to one side of the plane containing T2, or T2 lies strictly to one side of the plane containing T1, the triangles do not intersect. Otherwise, compute the line of intersection L between the planes. Let Ik be the interval (Tk inter L), k=1,2. Either interval may be empty. T1 and T2 intersect iff I1 and I2 overlap.
The Ocaml implementation of this test can be viewed online.
Compile with the command ocamlopt graphics.cmxa unix.cmxa collision.ml -o collision .
A quick comparison with the canonical implementation by Thomas Moeller s hows that my straightforward Ocaml implementation runs roughly 5 times as slowly as Moeller’s implementation in C.
My implementation currently handles coplanar triangles rather erratically, so I will either have to add a special function to check and handle coplanar triangles, or possibly check triangle normals for parallelism and perturb one of the triangles slightly to bring it out of plane before applying the normal test.
Bead on wire hoop demo
29 July 2007 Animation of the movement of a bead on a round frictionless wire hoop. more...Bead on wire hoop demo
closePreviously, I had written a simple 1d spring demo.. The next logical step was extension to three dimensions (wholly trivial) and the addition of constraints.
To start with, I begin with the canonical problem: a bead on a round frictionless wire hoop. (This is also equivalent to modeling the bob of a simple rigid pendulum). This is a path constraint. Movement is free along the path, but prohibited in any other direction. This can be represented by a constraint vector and a path. The constraint vector is the local radius of curvature and is perpendicular to the free path. The path represents all the positions in space a particle under that constraint may occupy.
For a bead on a hoop, the constraint vector is simply the radius of curvature, and for a hoop this is a vector of constant magnitude pointing towards the center of the hoop.
Any force acting on the bead produces an acceleration and over a period of time dt a displacement dx. This displacement causes the particle to travel in a straight line to x0, and (often) deviate from the path. So a vector can be constructed starting at the (deviated) position x0 along the constraint vector. This vector will intersect the path at a point x1. At this position a new velocity vector can be constructed tangent to the path (i.e. perpendicular to the constraint vector), with the same magnitude as the velocity vector at x0 (with, however, a different direction).
Source code can be viewed online.
Compile with ocamlopt unix.cmxa graphics.cmxa physics.ml -o physics or ocamlc unix.cma graphics.cma physics.ml -o physics
Simple 1d spring demo
21 July 2007 Animation of point spring unit masses with various evaluation methods (simple Euler, Newton-Stormer-Verlet, 4th order Runge-Kutta and a simple explicit Verlet integrator). more...Simple 1d spring demo
closeWhile playing around with a number of simple integrators I wrote a quick 1 dimensional spring demo. Four point spring unit masses are animated using various methods of evaluation (simple Euler, Newton-Stormer-Verlet, 4th order Runge-Kutta and a simple explicit Verlet integrator).
All four methods have the tendency to explode over time, although the Euler integrator does that the easiest. Somewhat to my surprise both Verlet integrators are more stable than the 4th order Runge Kutta integrator.
Source code can be viewed online.
Compile with ocamlopt unix.cmxa graphics.cmxa physics.ml -o physics or ocamlc unix.cma graphics.cma physics.ml -o physics
Using OpenGL with native OCaml Graphics toolkit
12 February 2007 This is a little experiment to combine OpenGL calls with Ocaml's native graphics toolkit more...Using OpenGL with native OCaml Graphics
closeCompiling:
Extract the files and run make. Edit the makefile if necessary, to ensure that the lineCLIB=GL is uncommented on Linux, and the line CLIB=opengl32 gdi32 is uncommented on Windows.
Link the resultant executable with libGL.a on X11, opengl32.lib and gdi32.lib on Windows.
Usage:
First set up your caml window withGraphics.open_graph ().>Next, call the function init_gl ()
After this you can (re)set the window title (if you set it previously it will be empty).
You may freely mix the Ocaml graphics functions with OpenGL calls.
Call swap_buffers () any time you need to flip the contents of your back buffer to the screen.
How does it work?
On both X11 and Win32 you can obtain pointers to
internal rendering surfaces of windows provided you can identify them by name. After opening the window with Graphics.open_graph (),
the function init_gl () gives the current window a (hopefully) unique title. Then C code is called
which searches through all available windows for a window with that particular name, gets pointers to its internal structure (both Win32 and
Xlib allow this) and sets it up for use as an OpenGL surface. This method works on Windows and X11; it may work on OS-X
(with a little tweaking in the #defines) but I have not tested that.
Tiny experiment with functional “widgets”
30 December 2006 This is a little experiment in abstracting away explicit state in functional programming. more...Tiny experiment with functional “widgets”
closedimension (top, left, width, height) and state (pressed, unpressed)
When a push button receives an input event, such as a mouse button click, it checks to see if that click occurred within its boundaries. In a stateful framework, the click toggles a mutable state variable from ‘unpressed’ to ‘pressed’, and this in turn triggers a redraw function to render the button in its pressed state (usually an event handler). However a simple push button can also be replaced by two widgets, representing the ‘pressed’, and ‘unpressed’ state respectively. The ‘unpressed’ widget will have a function to draw itself. Its input-processing function will check to see if a click occurred within its boundaries, and if not, return itself, or else return a ‘pressed’ widget. This ‘pressed’ widget will also know how to draw itself. Both ‘pressed’ and ‘unpressed’ widgets have no knowledge of how to draw each other, or have indeed any knowledge of each other.
The widget interface will consist of a type composed of a function that processes events (signature: fun mouse_x mouse_y mouse_button
key_pressed -> returns a new widget) and a function to draw the widget itself. II’m going to use closures to preserve the
strict function type signatures while allowing for latitude in information passing.
To this end I’ve written an simple test program,
consisting of two bare-bones “buttons". One is a static, square push button that changes colour from black to red
when it gets the focus. The other is a draggable, circular button that changes colour from black to red when it gets the focus, and
changes colour to yellow when it is being dragged around. Compile with ocamlc -o test graphics.cma test.ml.
Very short vector and matrix functions
25 August 2006 a short (less than 60 lines, including comments) linear algebra listing of one, two or three-liner vector and matrix functions more...Very short vector and matrix functions
closeAs a kind of finger exercise, a short (less than 60 lines, including comments) linear algebra listing of one, two or three-liner vector and matrix functions, including vector addition, subtraction, negation, scaling, dot product, matrix addition and subtraction, matrix-vector multiplication, matrix-matrix multiplication, matrix transpose, determinant, and matrix inverse.
These functions work (theoretically) on vectors of any dimension, and square matrices of any rank.
I wrote it to see how compact I could get the code using functional idioms, without intentional obfuscation. The code is therefore not the most efficient for either vectors or matrices of low dimension (where special casing would be of benefit), or high dimension (matrix inversion, for instance is done naively using the matrix’s adjugate and the performance of such an approach will not scale well at all with increasing dimension).
But it is short, anyhow.
glcaml and sdlcaml
closeThis project has moved to glcaml.sourceforge.net.
In the interests of reinventing the wheel where possible, I wrote OCaml bindings for the SDL libraries and OpenGL libraries over a couple of weekends.
The (automatically generated) OpenGL bindings cover OpenGL 1.1, 1.2, 1.3, 1.4, 1.5, 2.0 and most current non-platform-specific extensions. There are no dependencies whatsoever: the system opengl shared library is loaded dynamically, and the functions are called dynamically, so there is no need to link against import libraries.
The SDL bindings are fairly but not wholly complete; they are hand-written and functions are bound on an as-needed-by me basis. They are only dependent on the SDL main library and not on the mixer, ttf or image libraries. Because I wanted to have basic sound capabilities, the SDL_Audio modules are implemented, along with extra functions for panning and pitch shifting audio buffers.
Cell texture
12 May 2006 A cellular texture generator based on Blackpawn's article on cellular textures more...Cell texture
closeI saw this article on cellular textures and wrote an Ocaml cellular
texture generator (source code, public domain).Compile with
ocamlc graphics.cma celltexture.ml -o cell or ocamlopt graphics.cmxa celltexture.ml -o cell
Tiny OCaml pseudo-scheme interpreter
11 May 2006 A tiny OCaml pseudo-scheme interpreter based on Mark Probst's proof-of-concept interpreter more...Scheme interpreter
closeMark Probst wrote a very bare-bones proof-of-concept scheme interpreter in Objective Caml, licensed under the GPL. Well written, easy to extend. I rearranged the code a trifle, added floats and strings, apply, line comments, and a bunch of built-ins for a small project I was doing, and some basic error-messages (line number and approximate cause of whatever’s making the interpreter barf). There’s also an extract_string function in the parser that I’m pretty sure I didn’t write myself, but it’s been a year and I have no idea where I got it from. It’s not R5RS compliant, or R-anything-RS compliant; in fact since there are no guarantees that tail recursion will run in constant space it’s probably better not to think of it as a scheme implementation, per se. It’s more of a pseudo scheme.
The OCaml source code can be downloaded here, under the same licence as the original, the GPL.
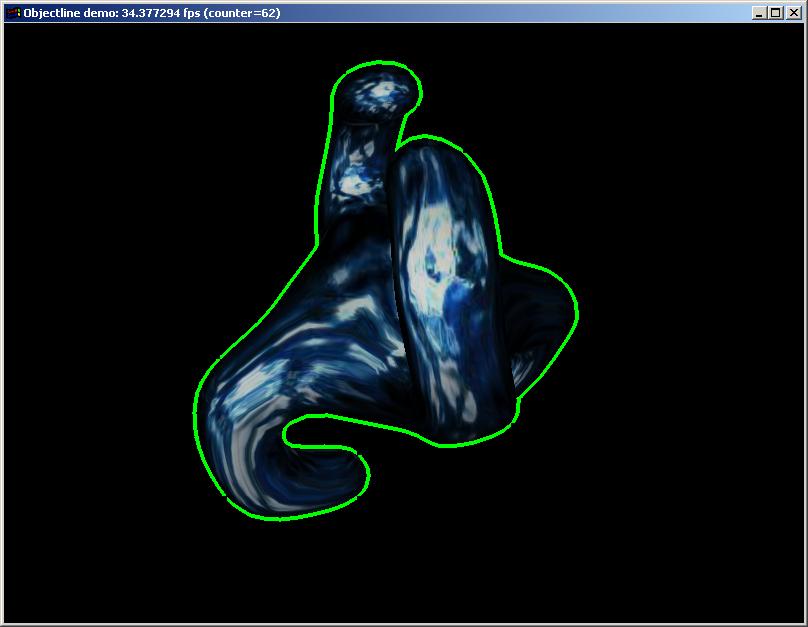
Building the demo
closeAdapted from the ObjectLine demo at frustum.org , an example using Ocaml and GLFW to render a silhouette around an object (using the stencil buffer).
Download objectline.tar.gz here.
Required:
- Ocaml version 3.06 or greater
- GLFW version 2.4.0 or greater
- CamlIDL version 1.0 or greater
- LablGL version 1.0 or greater
Building:
Unzipobjectline.tar.gz into a directory and edit the makefile depending on whether you are compiling for windows
(using MinGW) or Linux - there are two different sets of link libraries, so uncomment the appropriate path. Run make.
Building OGLFW
closeRequired:
- ocaml 3.08 (mingw version if building on windows)
- msys (optional, for building on windows )
- gcc 3.2 (may work with versions from 2.95.2 and up but this is untested)
- glfw 2.4.0 or later
- camlidl 1.01 or later
- lablGL 1.0 or later (for the examples mipmaps and triangles )
Usage
Unzip all files into a directory and run make.
The file keytest.ml is an example of how it may be used. Assumes both glfw and camlidl are installed and available.
ocamlopt -o keytest.exe oglfw.c glfw.mli glfw.ml keytest.ml -cclib -lglfw -cclib -lopengl32 -cclib -lglu32 -cclib -lcamlidl -cclib -lole32
ocamlopt -o keytest.exe oglfw.c glfw.mli glfw.ml keytest.ml -cclib -L/usr/X11R6/lib -cclib -lglfw -cclib -lGLU -cclib -lGL -cclib -lX11 -cclib -lXxf86vm -cclib -lXext -cclib -lpthread -cclib -lm -cclib -lcamlidl